Бинарная куча — различия между версиями
| Строка 1: | Строка 1: | ||
| − | == | + | == Куча == |
| − | + | Куча реализует очередь c приоритетами | |
| − | |||
| − | === | + | === Бинарная куча === |
| − | + | ==== Общее представление ==== | |
| − | + | Наша бинарная куча должна иметь эти функции:<br> | |
*Add(key, value)<br> | *Add(key, value)<br> | ||
(Вставка(ключ, значение))<br> | (Вставка(ключ, значение))<br> | ||
*Extract(key, value)<br> | *Extract(key, value)<br> | ||
| − | (Удаление(ключ, значение))< | + | (Удаление(ключ, значение)<br> |
| − | [[Файл:BinaryHeapLogo.png|400px|thumb|left]] | + | Всё работает за <math>\Theta(\logn)</math> |
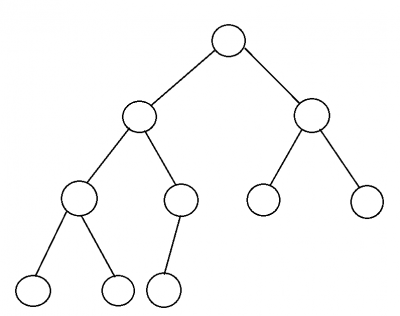
| + | [[Файл:BinaryHeapLogo.png|400px|без|thumb|left| двоичное дерево полное, означает, что заполнено слева направо и уровень не больше 1]] | ||
| + | ---- | ||
| + | ==== Вставка ==== | ||
| + | Посмотрим как можно добавить новый элемент:<br> | ||
| + | В начале просто допишем наш элемент k как ребёнка к любому нашему родителю, у которого слева(справа) нет ребёнка<br> | ||
| + | Но просто добавить его будет таким себе занятием, ибо может быть такое, что всё поломается, следовательно, нужно всё исправить<br> | ||
| + | Ибо нам необходимо, чтобы для каждого нашей ноды работал HeapProperity:<br> | ||
| + | [[Файл:HeapProperity.png|300px|без|thumb|left| Heap Properity]]<br> | ||
| + | Для этого применим алгоритм SiftUp(i): | ||
| + | <source lang="c++"> | ||
| + | void SiftUp(Node* i) | ||
| + | { | ||
| + | if(i != root) | ||
| + | while(p[i]->key > i->key) | ||
| + | swap(i) | ||
| + | return; | ||
| + | } | ||
| + | </source> | ||
| + | При первом заходе в цикл меняется что-то только, если наше новое <b>k</b> меньше чем <b>a</b>, <br> | ||
| + | Следовательно именно такой случай и рассмотрим:<br> | ||
| + | [[Файл:SiftUp.png|500px|без|thumb|left| Изменения после первого захода в цикл SiftUp]]<br> | ||
| + | Здесь, всё что оказалось ниже, чем <b>k</b> будет верно, следовательно нужно проверять выше<br> | ||
| + | Поэтому если <b>d</b> меньше, чем <b>k</b>, то снова заходим в цикл, иначе мы завершили<br> | ||
| + | ---- | ||
| + | ==== Извлечение ==== | ||
| + | Извлечение у нас будет осуществляться алгоритмом SiftDown<br> | ||
Версия 02:19, 6 марта 2020
Содержание
[убрать]Куча
Куча реализует очередь c приоритетами
Бинарная куча
Общее представление
Наша бинарная куча должна иметь эти функции:
- Add(key, value)
(Вставка(ключ, значение))
- Extract(key, value)
(Удаление(ключ, значение)
Всё работает за Невозможно разобрать выражение (Выполняемый файл <code>texvc</code> не найден; См. math/README — справку по настройке.): \Theta(\logn)
Вставка
Посмотрим как можно добавить новый элемент:
В начале просто допишем наш элемент k как ребёнка к любому нашему родителю, у которого слева(справа) нет ребёнка
Но просто добавить его будет таким себе занятием, ибо может быть такое, что всё поломается, следовательно, нужно всё исправить
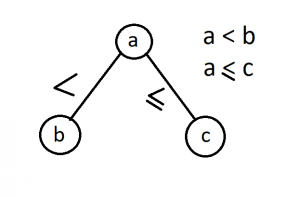
Ибо нам необходимо, чтобы для каждого нашей ноды работал HeapProperity:
Для этого применим алгоритм SiftUp(i):
void SiftUp(Node* i)
{
if(i != root)
while(p[i]->key > i->key)
swap(i)
return;
}
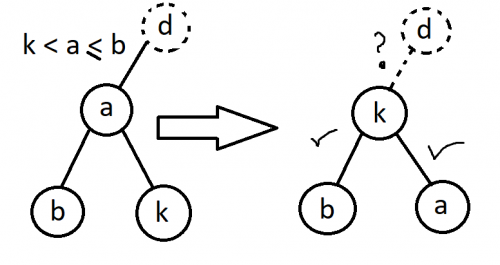
При первом заходе в цикл меняется что-то только, если наше новое k меньше чем a,
Следовательно именно такой случай и рассмотрим:
Здесь, всё что оказалось ниже, чем k будет верно, следовательно нужно проверять выше
Поэтому если d меньше, чем k, то снова заходим в цикл, иначе мы завершили
Извлечение
Извлечение у нас будет осуществляться алгоритмом SiftDown