Дерево отрезков — различия между версиями
(→Общая идея) |
(→Пример задачи) |
||
| (не показано 36 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
== Общая идея == | == Общая идея == | ||
| − | Очень похоже на sparse table - хотим предподсчитывать какие-то значения для отрезков, и обновлять их при изменении дерева.<br> | + | Очень похоже на sparse table - хотим предподсчитывать какие-то значения для отрезков, и обновлять их при изменении дерева.<br><br> |
''Замечание: рассматриваем на примере задачи RMQ из конспекта про sparse table'' | ''Замечание: рассматриваем на примере задачи RMQ из конспекта про sparse table'' | ||
| + | |||
| + | == Структура == | ||
| + | На нижнем уровне располагаются элементы массива, на уровень выше - узлы, в которых минимум из двух элементов, на уровень выше - минимум из соответствующих соседей предыдущего уровня и так далее. Рисунок для случая, когда количество элементов в массиве - степень двойки. | ||
| + | [[Файл:vis_tree.png]] | ||
| + | <br> | ||
| + | Разумеется, уровней всего O(log n). На i-м уровне, начиная от самого нижнего, n / 2^i элементов. Таким образом, все дерево можно построить (просто сумма членов геометрической прогрессии) за O(n). <br> | ||
| + | |||
| + | == Обработка запроса == | ||
| + | Общая идея: процедура getMin начинает от корня дерева и рекурсивно спускается в те отрезки, которые ее интересуют. Пусть мы находимся в вершине x, которая соответствует полуинтервалу TreeSeg = [L_tree, R_tree), а нам нужен минимум на полуинтервале QuerySeg = [L_q, R_q). Строго говоря, возможны три случая:<br> | ||
| + | 1. TreeSeg ⊆ QuerySeg. Тогда необходимо вернуть значение из вершины. <br> | ||
| + | 2. TreeSeg ⋂ QuerySeg = ∅. Необходимо вернуть какую-то большую константу IntMax, или какой-то флаг, показывающий, что отрезки не пересекаются - чтобы уже "вышестоящая вершина" думала над тем, что с этим знанием делать. <br> | ||
| + | 3. TreeSeg ⋂ QuerySeg ≠ ∅. Тогда, разумеется, для обработки запроса необходимо вернуть min (getMin (left_half (x)), getMin (right_half (x))). Заметим, что в силу того что left_half и right_half не пересекаются, мы в будущем сможем решать более сложные задачи с помощью этой же структуры. | ||
| + | |||
| + | {{Template:Lemma | ||
| + | |What = Лемма 1 | ||
| + | |Statement = Каждый такой запрос выполняется за O(log n). | ||
| + | |Proof = Понятно, что оценка асимптотики алгоритма сводится к подсчету количества рекурсий, которые наша процедура потребует для выполнения. Рассмотрим произвольный уровень нашего дерева при запросе. На нем мы сделаем не более двух рекурсий вниз по дереву (случай 3). Таким образом, количество рекурсий ограничено O(1) * O(height) = O(log n). | ||
| + | }} | ||
| + | |||
| + | == Изменение дерева == | ||
| + | ''Замечание: на данном этапе предлагается перейти к произвольной функции f элементов на отрезке. Разумеется, нам подойдут не все функции. Необходимо, чтобы эта функция была ассоциативной, поскольку иначе мы не сможет "расставлять скобки" при сведении этой задачи к меньшим. ''<br><br> | ||
| + | ''Оговорка: мы храним наше дерево в виде массива - по аналогии с бинарной кучей. ''<br><br> | ||
| + | Итак, обрабатываем запрос вида change (i, new_value). Существуют два подхода:<br> | ||
| + | 1. "Изменение снизу". <br> | ||
| + | Зная номер вершины i мы можем пересчитать все значения дерева, которые идут на пути от корня до этой вершины (напомним, что индекс родителя при нашей оговорке мы найдем как i / 2). Эта схема плоха тем, что работает только для случая, когда количество элементов - степень двойки. <br> | ||
| + | 2. "Изменение сверху". <br> | ||
| + | Аналогично процедуре обработки запроса, мы рекурсивно спускаемся в нужное нам поддерево, переподсчитываем там нашу функцию, после этого обновляем значение в текущей вершины и возвращаем его. | ||
| + | <br> | ||
| + | |||
| + | |||
| + | == Изменение элементов на подотрезке == | ||
| + | Пусть нам поступает запрос на присвоение всем элементам с индексами от L до R значения new_value. Вновь применим идею отложенной операции. Будем рекурсивно спускаться от корня пока весь соответствующий текущей вершине полуинтервал не будет лежать в [L, R); когда это произошло, сохраним в этой вершине запрос на изменение. <br> | ||
| + | Тогда нужно понять, как это повлияет на процедуру обработки запроса. Разумеется, изменится случай 1 - сейчас нам придется учитывать не только значение вершины, но и эту отложенную операцию, что, впрочем, несильно усложняет дело. Также необходимо в случае 3 "протолкнуть" отложенную операцию в сыновей. Понятно, что никакую асимптотику это нарушить не может. Но здесь важно не забыть после рассмотрения случаев 1, 2, 3 обновить значение в текущей вершине на основе вновь полученной информации о листьях данной вершины. И только после этого можно безопасно возвращаться к родительскому узлу. | ||
| + | |||
| + | == Персистентное дерево отрезков == | ||
| + | ''Замечание: здесь нам придется отказаться от идеи хранить структуру в виде массива, по аналогии с бинарной кучей.''<br><br> | ||
| + | Вдобавок к уже известным функциям и требованием иногда хочется уметь возвращаться к старой версии дерева. Таким образом, мы хотим добавить функцию checkout (version_number), где version_number - количество вызовов функции изменения дерева на подотрезке.<br> | ||
| + | Заметим, что при каждом вызове функции изменения дерева на подотрезке изменяется лишь O(log n) вершин. | ||
| + | <br> | ||
| + | [[Файл:ветвь.png]] | ||
| + | <br> | ||
| + | Более того, при каждой такой операции изменяется лишь один путь от корня до листа. Итак, мы может создавать новую версию этого пути, возвращая из функции change указатель на новую версию того самого пути. Тогда в каждой вершине на этом пути один из детей будет обновленным, а другой старым.<br><br> | ||
| + | Имея на руках систему контроля версий, мы можем считать нашу функцию f от полуинтервала исходного массива не только в актуальной версии дерева, но и в любой его версии, имея массив, в котором индекс - номер версии, а значение - соответствующая подветвь. | ||
| + | |||
| + | == Пример задачи == | ||
| + | Имеется статический массив. Запрос - количество элементов с индексами из [L, R), которые лежат во множестве {x, x+1, ... y-1, y}. <br><br> | ||
| + | '''Способ 1.''' <br> | ||
| + | Будем в каждой вершине хранить весь соответсвующий массив в отсортированном виде. Кажется, что о памяти лучше не думать, но на самом деле все относительно прилично: каждый элемент находится от корня на расстоянии O(log n) вершин, поэтому всего дополнительно затрачено будет O(n log n). После этого необходимо найти наибольший элемент, меньший x и наименьший, больший y в массиве нужной вершины. Тогда нужно просто вернуть количество элементов между этими только что найденными. <br><br> | ||
| + | '''Способ 2.''' <br> | ||
| + | Отсортируем элементы по возрастанию (разумеется, с сохранением первоначальной позиции элементов), получив массив S. Создадим пустой массив того же размера E, сделаем на нем дерево отрезков. После этого будем пробегать по массиву S и ставить в массив E единицы в соответствии и сохраненным ранее порядком. После этого достаточно сделать count (L, R, "≤ y") - count (L, R, "< x"), используя описанную выше систему контроля версий. Памяти мы тратим по-прежнему O(n log n), поскольку у нас n разных ветвей по log(n) каждая.<br><br> | ||
| + | |||
| + | ''Замечание: можно сделать дерево отрезков из деревьев отрезков, чтобы эффективно отвечать на похожие запросы в случае плоскости. '' | ||
Текущая версия на 12:57, 15 мая 2020
Содержание
[убрать]Общая идея
Очень похоже на sparse table - хотим предподсчитывать какие-то значения для отрезков, и обновлять их при изменении дерева.
Замечание: рассматриваем на примере задачи RMQ из конспекта про sparse table
Структура
На нижнем уровне располагаются элементы массива, на уровень выше - узлы, в которых минимум из двух элементов, на уровень выше - минимум из соответствующих соседей предыдущего уровня и так далее. Рисунок для случая, когда количество элементов в массиве - степень двойки.
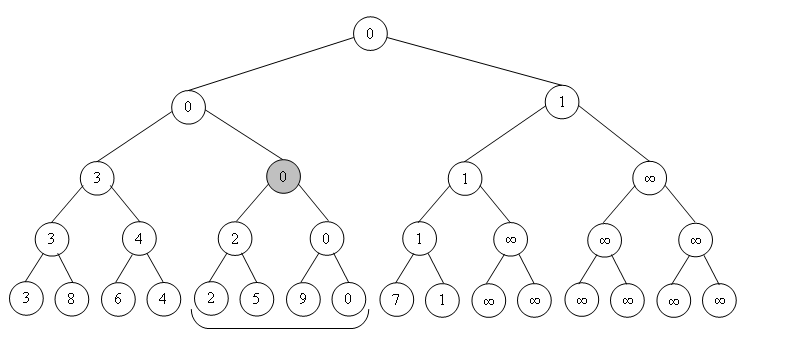
Разумеется, уровней всего O(log n). На i-м уровне, начиная от самого нижнего, n / 2^i элементов. Таким образом, все дерево можно построить (просто сумма членов геометрической прогрессии) за O(n).
Обработка запроса
Общая идея: процедура getMin начинает от корня дерева и рекурсивно спускается в те отрезки, которые ее интересуют. Пусть мы находимся в вершине x, которая соответствует полуинтервалу TreeSeg = [L_tree, R_tree), а нам нужен минимум на полуинтервале QuerySeg = [L_q, R_q). Строго говоря, возможны три случая:
1. TreeSeg ⊆ QuerySeg. Тогда необходимо вернуть значение из вершины.
2. TreeSeg ⋂ QuerySeg = ∅. Необходимо вернуть какую-то большую константу IntMax, или какой-то флаг, показывающий, что отрезки не пересекаются - чтобы уже "вышестоящая вершина" думала над тем, что с этим знанием делать.
3. TreeSeg ⋂ QuerySeg ≠ ∅. Тогда, разумеется, для обработки запроса необходимо вернуть min (getMin (left_half (x)), getMin (right_half (x))). Заметим, что в силу того что left_half и right_half не пересекаются, мы в будущем сможем решать более сложные задачи с помощью этой же структуры.
Изменение дерева
Замечание: на данном этапе предлагается перейти к произвольной функции f элементов на отрезке. Разумеется, нам подойдут не все функции. Необходимо, чтобы эта функция была ассоциативной, поскольку иначе мы не сможет "расставлять скобки" при сведении этой задачи к меньшим.
Оговорка: мы храним наше дерево в виде массива - по аналогии с бинарной кучей.
Итак, обрабатываем запрос вида change (i, new_value). Существуют два подхода:
1. "Изменение снизу".
Зная номер вершины i мы можем пересчитать все значения дерева, которые идут на пути от корня до этой вершины (напомним, что индекс родителя при нашей оговорке мы найдем как i / 2). Эта схема плоха тем, что работает только для случая, когда количество элементов - степень двойки.
2. "Изменение сверху".
Аналогично процедуре обработки запроса, мы рекурсивно спускаемся в нужное нам поддерево, переподсчитываем там нашу функцию, после этого обновляем значение в текущей вершины и возвращаем его.
Изменение элементов на подотрезке
Пусть нам поступает запрос на присвоение всем элементам с индексами от L до R значения new_value. Вновь применим идею отложенной операции. Будем рекурсивно спускаться от корня пока весь соответствующий текущей вершине полуинтервал не будет лежать в [L, R); когда это произошло, сохраним в этой вершине запрос на изменение.
Тогда нужно понять, как это повлияет на процедуру обработки запроса. Разумеется, изменится случай 1 - сейчас нам придется учитывать не только значение вершины, но и эту отложенную операцию, что, впрочем, несильно усложняет дело. Также необходимо в случае 3 "протолкнуть" отложенную операцию в сыновей. Понятно, что никакую асимптотику это нарушить не может. Но здесь важно не забыть после рассмотрения случаев 1, 2, 3 обновить значение в текущей вершине на основе вновь полученной информации о листьях данной вершины. И только после этого можно безопасно возвращаться к родительскому узлу.
Персистентное дерево отрезков
Замечание: здесь нам придется отказаться от идеи хранить структуру в виде массива, по аналогии с бинарной кучей.
Вдобавок к уже известным функциям и требованием иногда хочется уметь возвращаться к старой версии дерева. Таким образом, мы хотим добавить функцию checkout (version_number), где version_number - количество вызовов функции изменения дерева на подотрезке.
Заметим, что при каждом вызове функции изменения дерева на подотрезке изменяется лишь O(log n) вершин.
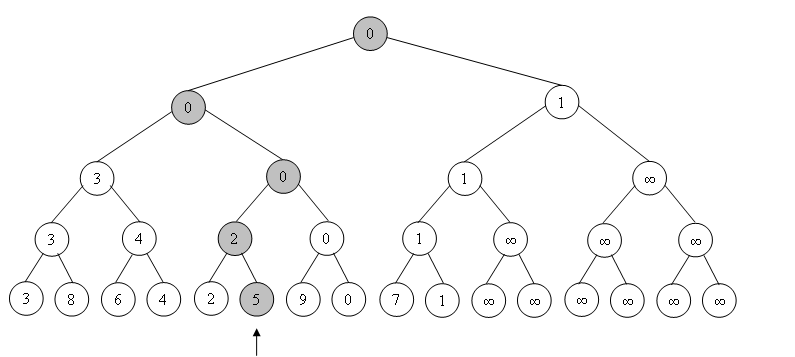
Более того, при каждой такой операции изменяется лишь один путь от корня до листа. Итак, мы может создавать новую версию этого пути, возвращая из функции change указатель на новую версию того самого пути. Тогда в каждой вершине на этом пути один из детей будет обновленным, а другой старым.
Имея на руках систему контроля версий, мы можем считать нашу функцию f от полуинтервала исходного массива не только в актуальной версии дерева, но и в любой его версии, имея массив, в котором индекс - номер версии, а значение - соответствующая подветвь.
Пример задачи
Имеется статический массив. Запрос - количество элементов с индексами из [L, R), которые лежат во множестве {x, x+1, ... y-1, y}.
Способ 1.
Будем в каждой вершине хранить весь соответсвующий массив в отсортированном виде. Кажется, что о памяти лучше не думать, но на самом деле все относительно прилично: каждый элемент находится от корня на расстоянии O(log n) вершин, поэтому всего дополнительно затрачено будет O(n log n). После этого необходимо найти наибольший элемент, меньший x и наименьший, больший y в массиве нужной вершины. Тогда нужно просто вернуть количество элементов между этими только что найденными.
Способ 2.
Отсортируем элементы по возрастанию (разумеется, с сохранением первоначальной позиции элементов), получив массив S. Создадим пустой массив того же размера E, сделаем на нем дерево отрезков. После этого будем пробегать по массиву S и ставить в массив E единицы в соответствии и сохраненным ранее порядком. После этого достаточно сделать count (L, R, "≤ y") - count (L, R, "< x"), используя описанную выше систему контроля версий. Памяти мы тратим по-прежнему O(n log n), поскольку у нас n разных ветвей по log(n) каждая.
Замечание: можно сделать дерево отрезков из деревьев отрезков, чтобы эффективно отвечать на похожие запросы в случае плоскости.