Красное-чёрное дерево — различия между версиями
(→Случай 2) |
|||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
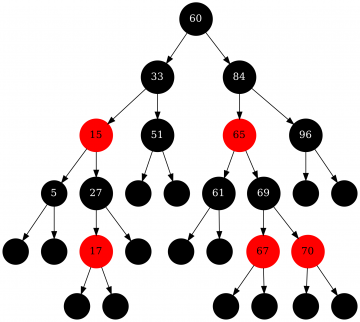
| − | [[File:rbtee_example.png|thumb|top|right|Пример КЧД]] | + | [[File:rbtee_example.png|thumb|top|right|upright=1.2|Пример КЧД]] |
| + | |||
'''Красно-чёрное дерево'''(англ. red-black tree) - самобалансирующееся бинарное дерево поиска (англ. Binary Search Tree, BST) со следующими свойствами: | '''Красно-чёрное дерево'''(англ. red-black tree) - самобалансирующееся бинарное дерево поиска (англ. Binary Search Tree, BST) со следующими свойствами: | ||
| Строка 8: | Строка 9: | ||
# У красной вершины оба ребёнка чёрные | # У красной вершины оба ребёнка чёрные | ||
# Чёрная высота каждой вершины определена корректно | # Чёрная высота каждой вершины определена корректно | ||
| − | |||
| − | |||
== Чёрная высота == | == Чёрная высота == | ||
| Строка 66: | Строка 65: | ||
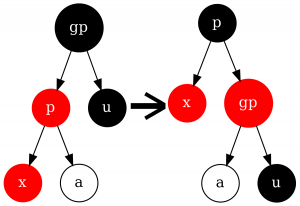
[[File:rbtee_insert_case2_subcase2.png|thumb|top|left|Подслучай 2]] | [[File:rbtee_insert_case2_subcase2.png|thumb|top|left|Подслучай 2]] | ||
| − | Легко заметить, что при таких действиях количество чёрных вершин на любом пути, проходящем через это поддерево не меняется. | + | Легко заметить, что при таких действиях количество чёрных вершин на любом пути, проходящем через это поддерево не меняется. Остальные свойства КЧД так же выполняются. В частности, корень поддерева $a$ должен быть чёрным. Теперь дерево сбалансированно. |
Текущая версия на 18:46, 15 апреля 2020
Красно-чёрное дерево(англ. red-black tree) - самобалансирующееся бинарное дерево поиска (англ. Binary Search Tree, BST) со следующими свойствами:
- Каждая вершина имеет цвет: красный или чёрный
- Корень дерева - чёрный
- У каждой нелистовой вершины ровно два ребёнка
- Все листья чёрные и фиктивные
- У красной вершины оба ребёнка чёрные
- Чёрная высота каждой вершины определена корректно
Содержание
[убрать]Чёрная высота
На пути от любой вершины красно-чёрного дерева до её потомка-листа одинаковое количество чёрных вершин.
Чёрная высота вершины $x$ (Обозначаем $bh(x)$) - количество чёрных вершин на пути от $x$ до любого её потомка-листа, не считая самого $x$.
Высота красно-чёрного дерева
Вставка
Рассмотрим, как поддерживать свойства красно-чёрного дереве при операции insert.
Производим вставку элемента в дерево как в любом BST и сразу красим его в красный цвет.
Тривиальные случаи
- $x$ - новый корень КЧД. Тогда красим его в чёрный цвет для поддрежания 2 свойства КЧД.
- Наш родитель $p$ - чёрный. Тогда вставка красного листа не нарушает свойств КЧД, а значит ничего делать не нужно.
Теперь если $p$ родитель $x$ оказался красным, то его родитель $gp$ обязан быть чёрным. Посмотрим на "дядюшку" $x$ - $u$.
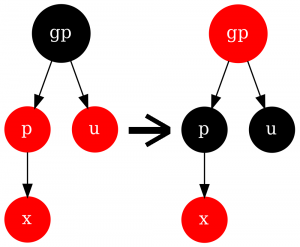
Случай 1
$u$ - красный (не фиктивный). Тогда красим $u$ и $p$ в чёрный, а $gp$ - в красный. После этого количество чёрных вершин на любом пути, проходящем через $gp$ не изменяется. Но могло нарушиться свойство 4, если родитель $gp$ оказался красным, или свойство 2, если $gp$ оказался чёрным. В первом случае конфликт был поднят выше по дереву - его можно исправить рекурсивно. Во втором случае мы просто красим $gp$ в чёрный цвет.
Случай 2
$u$ - чёрный (возможно фиктивный). Тогда далее будем считать, что $p$ - левый потомок $gp$. В ином случае дальнейшие действия следует отзеркалить.
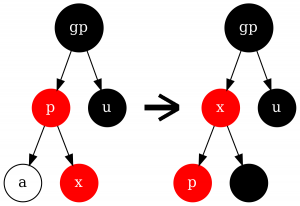
Рассмотрим два подслучая:
- $x$ - правый потомок $p$. В таком случае совершаем левое вращение с центром в $p$ и сводим этот случай к следующему ($p$ - новый $x$).
- $x$ - левый потомок $p$. В этом случае совершаем правое вращение с центром в вершине $gp$, предварительно покрасив $gp$ в красный, а $p$ - в чёрный.
Легко заметить, что при таких действиях количество чёрных вершин на любом пути, проходящем через это поддерево не меняется. Остальные свойства КЧД так же выполняются. В частности, корень поддерева $a$ должен быть чёрным. Теперь дерево сбалансированно.