Красное-чёрное дерево

Пример КЧД

Красно-чёрное дерево(англ. red-black tree) - самобалансирующееся бинарное дерево поиска (англ. Binary Search Tree, BST) со следующими свойствами:

• Каждая вершина имеет цвет: красный или чёрный
• Корень дерева - чёрный
• У каждой нелистовой вершины ровно два ребёнка
• Все листья чёрные и фиктивные
• У красной вершины оба ребёнка чёрные
• Чёрная высота каждой вершины определена корректно

Чёрная высота

На пути от любой вершины красно-чёрного дерева до её потомка-листа одинаковое количество чёрных вершин.

Чёрная высота вершины $x$ (Обозначаем $bh(x)$) - количество чёрных вершин на пути от $x$ до любого её потомка-листа, не считая самого $x$.

Лемма 1

В поддереве вершины $x$ как минимум $2^{bh(x)} - 1$ вершин.

Доказательство

Пусть $c(x)$ - количество вершин в поддереве x.

Индукция по $h(x)$:

• База: $h(x) = 0$ - очевидное отверждение
• Переход:
  К потомкам $x$ - $y$ и $z$ применимо предположение индукции.
  Заметим также, что $bh(y) \geq bh(x) - 1$ и $bh(z) \geq bh(x) - 1$.
  Тогда $c(x) \geq 1 + 2^{bh(y)} - 1 + 2^{bh(z)} - 1 \geq 2^{bh(x) - 1} + 2^{bh(x) - 1} - 1 \eq 2^{bh(x)} - 1$

Высота красно-чёрного дерева

Лемма 2

Если $T$ - красно-чёрное дерево, то $h(T) \leq log_2 (n + 1)$.

Доказательство

Из свойств дерева, на любом пути из вершины $x$ в лист красных вершин не больше чёрных.
Отсюда $h(x) \leq 2 bh(x)$. Тогда по Л1 $n \geq 2^{bh(root)} - 1$.
Отсюда $log_2 (n + 1) \geq bh(root) \geq 0.5 \cdot h(root) \rightarrow h(root) \leq 2 \cdot log_2 (n + 1)$

Вставка

Рассмотрим, как поддерживать свойства красно-чёрного дереве при операции insert.

Сразу после insert

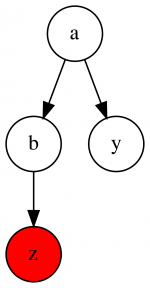
Производим вставку элемента в дерево как в любом BST и сразу красим его в красный цвет. Вставленный элемент - $z$, рассмотрим его "дядюшку" $y$ и разберём случаи, в которых после такой вставки могут нарушиться свойства нашего дерева.