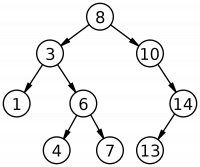
Наивное дерево поиска

Определение и свойства

Двоичное дерево поиска (англ. - Binary Search tree - BST) - структура данных двоичное дерево, для любого узла которого выполняются следующие свойства:

1. Оба узла поддерева являются двоичными деревьями поиска;
2. Все значения ключей левого поддерева меньше ключа узла;
3. Все значения ключей правого поддерева больше ключа узла.

Двоичное дерево поиска

Операции над деревом

Поиск

Алгоритм

Поиск узла по заданному ключу можно осуществлять рекурсивно, начиная из вершины.

1. Если узел отсутствует, возвращаем нулевой указатель.
2. Если значение в узле равно ключу, возвращаем указатель на узел.
3. Если значение в узле больше ключа, запускаем поиск по ключу в левом поддереве.
4. Если значение в узле меньше ключа, запускаем поиск по ключу в правом поддереве.

Реализация на языке C

node_t* find (node_t* head, elem_t key) {
 if (!head)
  return NULL;
 if (head->data == key)
  return head;
 if (head->data > key)
  return find(head->left, key);
 if (head->data < key)
  return find(head->right, key);
}

Вставка

Алгоритм

Вставку ключа, как и поиск, будем осуществлять рекурсивно, начиная из вершины.

1. Если узел пустой, вставляем на его место новый узел с ключом.
2. Если ключ равен значению в узле, возвращаемся и ничего не добавляем.
3. Если ключ меньше значения в узле, рекурсивно вызываем вставку в левом поддереве.
4. Если ключ больше значения в узле, рекурсивно вызываем вставку в правом поддереве.

Реализация на языке C

void insert (node_t* head, T key) {
  if (head->data == key)
   return;
  if (head->data > key) {
   if (head->left == null) {
    node_t* newnode = node_create(key);
    newnode->parent = head;
    head->left = newnode;
    return;
   }
   insert(head->left, key);
  }
  if (head->data < key) {
   if (head->right == null) {
    node_t* newnode = node_create(key);
    newnode->parent = head;
    head->right = newnode;
    return;
   }
   insert(head->right, key);
  }
}

Удаление

Алгоритм

Удаление вершины по ключу будем также осуществлять рекурсивно, начиная из вершины.

1. Если вершина пуста, возвращаемся.
2. Если вершина пуста